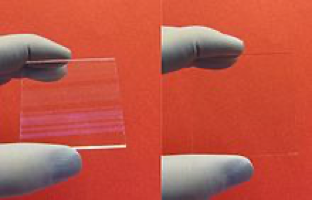
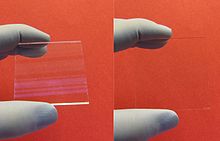
When I am on a plane, in an airport or at a dinner and people ask me what I do, I respond by saying, “I bend light and count molecules for a living.” This is a pretty grand statement and most times I am proud of the complex, medically beneficial science that I am in. Then I hear from people about the glare reducer or doctors talking about a patient looking better because the lens won’t reflect so much. This highly complicated and very scientific light filter has been reduced to a glare reducer.
In this article I would like to discuss the complexity of the coating, the difficulty of putting something so complex on variable index materials with varying geometries, and what is actually happening to the light, energy, photons, and electromagnetic fields relative to a beam of light.
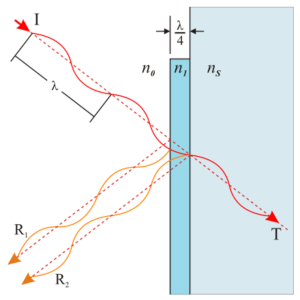
The above is a single light wave traveling through a hardcoat and a lens (from John E. Davis, Multilayer Reflectivity). As you can see, each surface has several reflections and transmissions (refractions). All of these must be accounted for in an AR coating design.
The term anti-reflective (AR) coating is deceiving. What it should be called is a “transmission booster” or “light booster for a lens. What it does, in effect, is Increase Light Transmission through the lens. This is the single most important thing an AR coating does. Lenses transmit between 85%-96% of the available light to the eye. AR coated lenses transmit 98%-99.5% of light through to the eye. This translates into many positive effects, most importantly in low light conditions such as night driving.
How does an AR coating work?
(http://en.wikipedia.org/wiki/Anti-reflective_coating)
Whenever a ray of light moves from one medium to another (for example, when light enters a sheet of glass after travelling through air), some portion of the light is reflected from the surface (known as the interface) between the two media. This can be observed when looking through a window, for instance, where a (weak) reflection from the front and back surfaces of the window glass can be seen. The strength of the reflection depends on the refractive indices of the two media as well as the angle of the surface to the beam of light. The exact value can be calculated using the Fresnel equations.
When the light meets the interface at normal incidence (perpendicularly to the surface), the intensity of light reflected is given by the reflection coefficient or reflectance, R:
where n0 and nS are the refractive indices of the first and second media, respectively. The value of R varies from 0 (no reflection) to 1 (all light reflected) and is usually quoted as a percentage. Complementary to R is the transmission coefficient or transmittance, T. If absorption and scattering are neglected, then the value T is always 1–R. Thus if a beam of light with intensity I is incident on the surface, a beam of intensity RI is reflected, and a beam with intensity TI is transmitted into the medium.
For the simplified scenario of visible light travelling from air (n0≈1.0) into common glass (nS ≈ 1.5), value of R is 0.04, or 4% on a single reflection. So at most 96% of the light (T = 1 − R = 0.96) actually enters the glass, and the rest is reflected from the surface. The amount of light reflected is known as the reflection loss.
In the more complicated scenario of multiple reflections, say with light travelling through a window, light is reflected both when going from air to glass and at the other side of the window when going from glass back to air. The size of the loss is the same in both cases. Light also may bounce from one surface to another multiple times, being partially reflected and partially transmitted each time it does so. In all, the combined reflection coefficient is given by 2R/(1 + R). For glass in air, this is about 7.7%.
The use of an intermediate layer to form an anti-reflection coating can be thought of as analogous to the technique of impedance matching of electrical signals. Further reduced reflection could in theory be made by extending the process to several layers of material, gradually blending the refractive index of each layer between the index of the air and the index of the substrate.
Practical anti-reflection coatings, however, rely on an intermediate layer not only for its direct reduction of reflection coefficient, but also use the interference effect of a thin layer. Assume the layer’s thickness is controlled precisely, such that it is exactly one quarter of the wavelength of light in the layer (λ/4 = λ0/(4n1), where λ0 is the vacuum wavelength). The layer is then called a quarter-wave coating. For this type of coating a normally incident beam I, when reflected from the second interface, will travel exactly half its own wavelength further than the beam reflected from the first surface, leading to destructive interference. This is also true for thicker coating layers (3λ/4, 5λ/4, etc.), however the anti-reflective performance is worse in this case due to the stronger dependence of the reflectance on wavelength and the angle of incidence.
If the intensities of the two beams R1 and R2 are exactly equal, they will destructively interfere and cancel each other since they are exactly out of phase. Therefore, there is no reflection from the surface, and all the energy of the beam must be in the transmitted ray.
Counting Molecules-how do we practically make an AR coating?
The most common method for AR coating Ophthalmic lenses is Physical Vapor Deposition (either Electron Beam Gun or Sputter Gun evaporation, here Electron Beam Evaporation is discussed). In this method, we take a solid, organic material and heat it to its boiling point (for most not all materials, some are sublimated which skips the liquid phase). The material then gives off a vapor in a deposition plume (which is the material in molecular form in the gas phase). In order for the molecules in the deposition plume to travel the distance from the evaporation source to the lens, we must remove the molecules from the pathway between the two. This is why we AR coat lenses in a vacuum chamber.
The molecules come in contact with a surface and return (referred to as growing the film) to a solid phase. In order to control how much material goes onto the lens, we must count the molecules being deposited.
To count these molecules and the resultant thickness (in nanometers) we typically use a quartz crystal microbalance. This is how it works (once again an explanation from Wikipedia http://en.wikipedia.org/wiki/QCM):
Quartz is one member of a family of crystals that experience the piezoelectric effect. The piezoelectric effect has found applications in high power sources, sensors, actuators, frequency standards, motors, etc., and the relationship between applied voltage and mechanical deformation is well known; this allows probing an acoustic resonance by electrical means. Applying alternating current to the quartz crystal will induce oscillations. With an alternating current between the electrodes of a properly cut crystal, a standing shear wave is generated. The Q factor, which is the ratio of frequency and bandwidth, can be as high as 106. Such a narrow resonance leads to highly stable oscillators and a high accuracy in the determination of the resonance frequency. The QCM exploits this ease and precision for sensing. Common equipment allows resolution down to 1 Hz on crystals with a fundamental resonant frequency in the 4 – 6 MHz range. A typical setup for the QCM contains water cooling tubes, the retaining unit, frequency sensing equipment through a microdot feed-through, an oscillation source, and a measurement and recording device.
The frequency of oscillation of the quartz crystal is partially dependent on the thickness of the crystal. During normal operation, all the other influencing variables remain constant; thus a change in thickness correlates directly to a change in frequency. As mass is deposited on the surface of the crystal, the thickness increases; consequently the frequency of oscillation decreases from the initial value. With some simplifying assumptions, this frequency change can be quantified and correlated precisely to the mass change using Sauerbrey’s equation.
Now that we understand how we count the molecules and change light, we can start to see the implications. To create a coating that reduces High Energy Visible light or stops reflecting Ultraviolet light is possible. There all sorts of additional medical benefits, as well as cosmetic and structural (ease of cleaning, scratch resistance, etc.) benefits to AR coatings. But, if we can control a billionth of a meter consistently and control the result of light impacting a surface, there are many moremedical and optical benefits that will come.
In conclusion, it takes computers to do most of the computational math behind AR coatings and to count the molecules that make up an AR coating. To be sure, there is a lot of math and physics behind these complicated filters. In the simplest terms, we are making a coating with a thickness of billionths of a meter, we are bending light to eliminate reflection, and we are taking the energy from the reflected photons and transferring it to the transmitted photons. There is a lot going on to make these coatings work. All of this so that the patients can see better. Isn’t it about time we stopped talking about the cosmetic benefits and what color it is, and started teaching the patients about the medical benefits and complexity of these coatings so that they understand why they need it? ? When they are educated, they will be lifelong converts to AR coating.