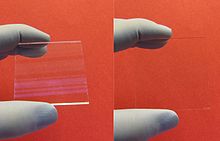
When I find myself on a plane, in an airport, or at a dinner, and people inquire about my profession, I respond by stating, “I bend light and count molecules for a living.” This statement, though grand, encapsulates the intricacies of the medically beneficial science in which I am engaged. However, it often gets reduced to discussions about glare reduction or doctors praising a patient’s improved appearance due to minimized lens reflections. The highly sophisticated and scientific light filter I work with is sometimes oversimplified as a mere glare reducer.
In this article, I aim to delve into the complexity of the coating, exploring the challenges of applying such a intricate technology to variable index materials with diverse geometries. Furthermore, I’ll unravel the intricate processes affecting light, energy, photons, and electromagnetic fields as they interact with a beam of light.
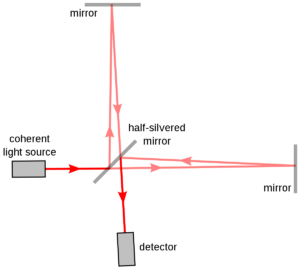The diagram illustrates a single light wave traversing through a hardcoat and a lens (adapted from John E. Davis, Multilayer Reflectivity). Each surface exhibits multiple reflections and transmissions (refractions), all of which must be considered in the design of an anti-reflective (AR) coating.
The term “anti-reflective” coating can be misleading. A more accurate description would be a “transmission booster” or “light booster for a lens.” Essentially, an AR coating increases light transmission through the lens, a critical function that enhances vision. While lenses typically transmit between 85% and 96% of available light to the eye, AR-coated lenses transmit an impressive 98% to 99.5%. This heightened light transmission has numerous positive effects, especially in low-light conditions such as night driving.
How Does an AR Coating Work?
Link to Wikipedia on Anti-reflective coating
When light transitions from one medium to another (e.g., entering a sheet of glass from air), a portion is reflected at the interface between the two media. The strength of this reflection depends on the refractive indices and the angle of the surface to the light beam. The term “anti-reflective” can be deceiving, as the primary function of an AR coating is to increase light transmission through the lens. In practical terms, this means that AR-coated lenses transmit 98% to 99.5% of light to the eye, resulting in numerous benefits, particularly in low-light conditions like night driving.
When the light meets the interface at normal incidence (perpendicularly to the surface), the intensity of light reflected is given by the reflection coefficient or reflectance, R: where n0 and nS are the refractive indices of the first and second media, respectively. The value of R varies from 0 (no reflection) to 1 (all light reflected) and is usually quoted as a percentage. Complementary to R is the transmission coefficient or transmittance, T. If absorption and scattering are neglected, then the value T is always 1–R. Thus if a beam of light with intensity I is incident on the surface, a beam of intensity RI is reflected, and a beam with intensity TI is transmitted into the medium.
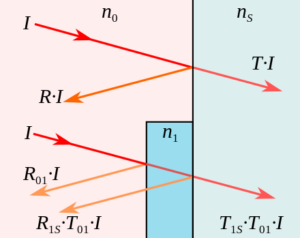For the simplified scenario of visible light traveling from air (n0≈1.0) into common glass (nS ≈ 1.5), value of R is 0.04, or 4% on a single reflection. So at most 96% of the light (T = 1 − R = 0.96) actually enters the glass, and the rest is reflected from the surface. The amount of light reflected is known as the reflection loss.
In the more complicated scenario of multiple reflections, say with light traveling through a window, light is reflected both when going from air to glass and at the other side of the window when going from glass back to air. The size of the loss is the same in both cases. Light also may bounce from one surface to another multiple times, being partially reflected and partially transmitted each time it does so. In all, the combined reflection coefficient is given by 2R/(1 + R). For glass in air, this is about 7.7%.
The use of an intermediate layer to form an anti-reflection coating can be thought of as analogous to the technique of impedance matching of electrical signals. Further reduced reflection could in theory be made by extending the process to several layers of material, gradually blending the refractive index of each layer between the index of the air and the index of the substrate.
Practical anti-reflection coatings, however, rely on an intermediate layer not only for its direct reduction of reflection coefficient, but also use the interference effect of a thin layer. Assume the layer’s thickness is controlled precisely, such that it is exactly one quarter of the wavelength of light in the layer (λ/4 = λ0/(4n1), where λ0 is the vacuum wavelength). The layer is then called a quarter-wave coating. For this type of coating a normally incident beam I, when reflected from the second interface, will travel exactly half its own wavelength further than the beam reflected from the first surface, leading to destructive interference. This is also true for thicker coating layers (3λ/4, 5λ/4, etc.), however the anti-reflective performance is worse in this case due to the stronger dependence of the reflectance on wavelength and the angle of incidence.
If the intensities of the two beams R1 and R2 are exactly equal, they will destructively interfere and cancel each other since they are exactly out of phase. Therefore, there is no reflection from the surface, and all the energy of the beam must be in the transmitted ray.
Counting Molecules – Practical Aspects of AR Coating
The most common method for applying AR coatings to ophthalmic lenses is Physical Vapor Deposition, specifically Electron Beam Evaporation (discussed here). In this method, a solid organic material is heated to its boiling point, producing a vapor in a deposition plume. The coating process takes place in a vacuum chamber to ensure the molecules reach the lens without interference.
To measure the molecules’ deposition and resulting thickness in nanometers, a quartz crystal microbalance is commonly used. The piezoelectric effect in quartz crystals induces oscillations when alternating current is applied. The frequency of oscillation is dependent on the crystal’s thickness, allowing precise measurement of the mass change as molecules are deposited.
Understanding the molecular counting process and its impact on light allows for the creation of coatings with specific medical, cosmetic, and structural benefits. Controlling thickness at the nanometer level enables the reduction of High Energy Visible light or prevention of Ultraviolet light reflection, leading to various medical advantages.
In conclusion, the complexity of AR coatings involves intricate computations and molecular counting, often facilitated by computers. Despite the sophisticated physics and mathematics behind these filters, the ultimate goal is simple: creating a coating with a thickness of billionths of a meter to bend light, eliminate reflection, and transfer energy from reflected to transmitted photons. Educating patients about the medical benefits and complexity of these coatings ensures informed decisions and lifelong appreciation for AR coating.
